топологического пространства X - целочисленный инвариант dim X, определяемый следующим образом. Тогда и только тогда dim X = -1, когда . О непустом тополо-гич. пространстве Xговорят, что оно не более чем n-мерно, и пишут dim , если в любое конечное открытое покрытие пространства Xможно вписать конечное открытое покрытие пространства Xкратности 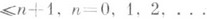. Если 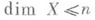для нек-рого п=-1,0,1,. . ., то пространство Xназ. конечномерным, пишется 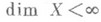и считается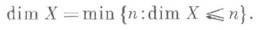

При этом если dim X = n, то пространство наз. n-мерным. Понятие Р. топологич. пространства обобщает элементарно-геометрич. понятие числа измерений евклидова пространства (и полиэдра), т. к. размерность n-мерного евклидова пространства (и любого n-мерного полиэдра) равна n (теорема Брауэра - Лебега).

Важность понятия Р. топологич. пространства выявляется теоремой Нёбелинга - Понтрягина - Гуревича -Куратовского: n-мерное метризуемое со счетной базой пространство вкладывается в (2n+1)-мерное евклидово пространство. Таким образом, класс пространств, топологически эквивалентных подпространствам всевозможных n-мерных евклидовых пространств, n=1, 2,. . ., совпадает с классом конечномерных метризуемых пространств со счетной базой.

Размерность dim Xиногда наз. лебеговой, т. <к. ее="" определение="" отталкивается="" от="" т="" е="" о="" р="" е="" м="" ы="" лебега="" "о="" мостовых":="" n-мерный="" куб="" для="" любого="" e>0="" обладает="" конечным="" замкнутым="" кратности=""> 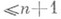покрытием с диаметром элементов <e; существует такое e₀>0, что кратность любого конечного замкнутого покрытия n-мерного куба 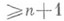, если диаметр элементов этого покрытия <e₀.

К определению Р. топологич. пространства возможен другой - индуктивный - подход (см. Индуктивная размерность), основанный на разбиении пространства подпространствами меньшего числа измерений. Этот подход к понятию Р. восходит к А. Пуанкаре (Н. Poincare), Л. Брауэру (L. Brouwer), П. С. Урысону и К. Менгеру (К. Menger). В случае метризуемых пространств он эквивалентен лебеговскому.

Основы теории Р. были заложены в 1-й пол. 20-х гг. 20 в. в работах П. С. Урысона и К. Менгера. К кон. 30-х гг. была построена теория Р. метризуемых пространств со счетной базой, а к нач. 60-х гг.- теория Р. любых метризуемых пространств.

Ниже все рассматриваемые топологич. пространства считаются нормальными и хаусдорфовыми. В этом случае в определении Р. без ущерба вписываемые открытые покрытия можно заменить на замкнутые.

Лебегов подход к определению Р. (в отличие от индуктивного подхода) позволяет в случае любых рассматриваемых пространств геометризовать понятие Р. посредством сравнения исходного топологич. пространства с простейшими геометрич. образованиями - полиэдрами. Грубо говоря, пространство n-мерно тогда и только тогда, когда оно сколь угодно мало отличается от n-мерного полиэдра. Точнее, имеет место теорема Александрова об w-отображениях: тогда и только тогда 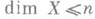, когда для любого конечного открытого покрытия и пространства Xсуществует w-отображение пространства Xна не более чем n-мерный, n=0,1,2,. . ., (компактный) полиэдр. Особую наглядность сформулированная теорема приобретает в случае компактов: для компакта Xтогда и только тогда dim , когда для любого e>0 существует e-отображение компакта на не более чем n-мерный полиэдр. Если еще Xлежит в евклидовом или гильбертовом пространстве, то e-отображение можно заменить e-сдвигом (теорема Александрова об e-о тображениях и e-сдвигах).

Следующее утверждение позволяет выяснить, какова Р. пространства, посредством его сравнения со всевозможными n-мерными кубами: тогда и только тогда dim , когда пространство обладает существенным отображением на n-мерный куб, n=0,1,2,. . . (теорема Александрова о существенных отображениях).

Этой теореме можно придать следующую форму. Тогда и только тогда 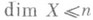, когда для любого замкнутого в Xмножества Аи любого непрерывного отображения 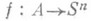в n-мерную сферу существует непрерывное продолжение 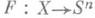, n=0,1,. . ., отображения f.

Следующая характеристика Р. указывает на роль этого понятия в вопросах существования решений систем уравнений: тогда и только тогда dim , n=1,2,..., когда в Xсуществует такая система дизъюнктных пар замкнутых множеств A_i, B_i, i=l,. . ., n, что для любых непрерывных на Xфункций f_i, удовлетворяющих условию 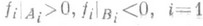,. . ., п, найдется точка 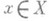, в к-рой f_i(x) = 0, i=1,. . ., (т е о р е м а Отто - Эйленберга - Хеммингсена о перегородках).

Одно из важнейших свойств Р. выражает теорема суммы Менгера - Урысона - Чеха: если пространство Xесть конечная или счетная сумма своих замкнутых подмножеств размерности 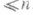, то и 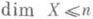, n=0,1,. . . В этой теореме можно условие конечности или счетности суммы заменить условием ее локальной конечности. Аналогичное теореме суммы утверждение для большой и малой индуктивных Р. не выполняется уже в классе бикомпактов. Следующие утверждения принадлежат к числу основных общих фактов теории Р. и позволяют сводить рассмотрение любых пространств к рассмотрению бикомпактов. Для любого нормального пространства

а) dim bX =dim X,Ind bX = Ind X, где b Х- максимальное бикомпактное расширение Стоуна -- Чеха пространства X;в то же время неравенство ind bХ> >ind X =Ind X возможно;

б) существует бикомпактное расширение bХ пространства X, вес к-рого 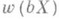равен весу 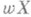, и размерность dim bХ равна размерности dim X;аналогичное утверждение верно и для большой индуктивной Р. Особенно интересен случай счетного веса пространства, т. к. в этом случае расширение bХ метризуемо.

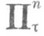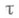Утверждение б) может быть усилено следующим предложением: для. любого n=0,1,. . . и любой бесконечной мощности существует бикомпакт веса и размерности 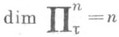, содержащий гомеоморфный образ любого нормального пространства Xвеса 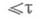и размерности 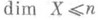(теорема об универсальном бикомпакте данного веса и размерности). Аналогичное утверждение верно и для большой индуктивной Р. При этом в качестве 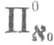можно взять канторово совершенное множество, а в качестве 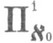- менгеровскую универсальную кривую.

Казалось бы, что Р. должна обладать свойством монотонности: dim 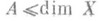, если АМ Х. Это так, если а) множество Азамкнуто в Xили сильно паракомпактно, или б) пространство Xметризуемо (и даже совершенно нормально). Однако уже для подмножества Анаследственно нормального пространства Xможет быть dim A>dim Xи Ind A>Ind Х. Но всегда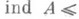 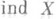при АМ Х.

Одним из важнейших вопросов теории Р. является поведение Р. при непрерывных отображениях. В случае замкнутых отображений (к ним принадлежат и все непрерывные отображения бикомпактов) ответ дается формулами В. Гуревича (W. Hurewicz), полученными им первоначально в классе пространств со счетной базой.

Формула Гуревича для повышающих размерность отображений: если отображение 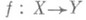непрерывно и замкнуто, то кратность , где кратность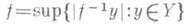

Формула Гуревича для понижающих размерность отображений: для непрерывного замкнутого отображения 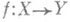на па-ракомпакт Yвыполняется неравенство

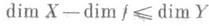(1)

где

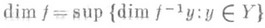
Для произвольного нормального пространства Yэта формула, вообще говоря, неверна.

В случае непрерывных отображений конечномерных компактов установлено, что непрерывное отображение f размерности dim f=k является суперпозицией kнепрерывных отображений размерности 1 (это - уточнение формулы (1) и аналог того факта, что k-мерный куб есть произведение kотрезков).

В случае открытых отображений можно показать, что образ нульмерного бикомпакта нульмерен и в то же время гильбертов кирпич есть образ одномерного компакта, даже если соответствующее отображение f имеет размерность dim f, равную нулю. Однако в случае открытого отображения 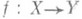бикомпактов Xи Yкратности 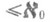выполняется равенство dim X=dim Y.

Поведение Р. при взятии топологич. произведения описывают следующие утверждения:

а) существуют такие конечномерные компакты Xи Y, что ;

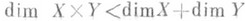б) если один из сомножителей произведения 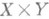бикомпактен или метризуем, то ;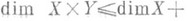

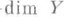в) существуют такие нормальные пространства Xи Y, что

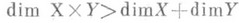
В случае бикомпактных Xи Y всегда 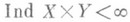, если 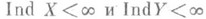. , но может быть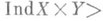 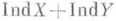. Если же бикомпакты XиYсовершенно нормальны или одномерны, то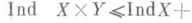 .
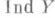