в т е о р и и дифференциальных уравнений - приемы построения приближенных решений дифференциальных уравнений и систем, зависящих от параметра.

1) М. п. м. для обыкновенных дифференциальных уравнении. Обыкновенные дифференциальные уравнения, к к-рым приводят прикладные задачи, обычно содержат один или несколько параметров. Параметр может входить также в начальные данные или граничные условия. Поскольку найти точное решение дифференциального уравнения можно лишь для отдельных весьма частных классов, возникла задача о построении приближенного решения. Одна из типичных постановок ее такова: уравнение и начальные (граничные) условия содержат параметр l и решение известно (или его можно считать известным) при l=l₀;требуется построить приближенное решение при значениях параметра l, близких к l₀, т. е. построить асимптотику решения при где e=l-l₀ - малый параметр. М. п. м., возникший в связи с задачей трех тел небесной механики, восходит к Ж. Д'Аламберу (J. D'Alembert) и интенсивно развивается с кон. 19 в.

Ниже используются следующие обозначения: t- независимое переменное, e>0 - малый параметр, I - отрезок знак - означает асимптотич. равенство. Все векторные и матричные функции, входящие в уравнения и в граничные условия, предполагаются гладкими (класса ) по совокупности переменных в рассматриваемой области (по e - при или ).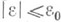

1. Задача Коши для системы n-го порядка:

Пусть решение предельной задачи (т. е. задачи, получающейся из (1) при e=0) существует и единственно при _ Тогда для решения x(t, е).задачи (1) справедливо асимптотич. разложение при

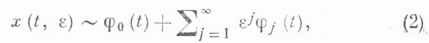
равномерное по Этот факт вытекает из теоремы о гладкой зависимости от параметра решений системы обыкновенных дифференциальных уравнений. Если вектор-функции f и х ₀ голоморфны при 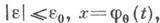то ряд (2) сходится к решению x(t, е) при достаточно малых |e| равномерно по 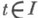(теорема Пуанкаре). Аналогичные результаты справедливы и для краевой задачи для системы вида (1), если решение соответствующей предельной задачи существует и единственно.

Различают два вида зависимости уравнения (или системы) от малого параметра - регулярную и сингулярную. Система в нормальной форме регулярно зависит от параметра e, если все правые ее части - гладкие функции от e при малых в противном случае система зависит от параметра 8 сингулярно. При регулярной зависимости системы от e решение задачи с параметром на конечном отрезке по t, как правило, равномерно стремится при к решению предельной задачи.

2. В линейной теории рассматриваются сингулярно зависящие от параметра е системы n-го порядка

где элементы -матрицы Аи компоненты вектора f- комплекснозначные функции. Центральная задача линейной теории - построение такой фундаментальной системы решений (ф. с. р.) однородной системы (т. е. при ), для к-рой асимптотика при известна на всем отрезке I.

Основным результатом линейной теории является следующая теорема Биркгофа. Пусть: 1) собственные значения матрицы A(t,0) различны при 2) величины

не меняют знак. Тогда существует ф. с. p. x₁(t,e), ..., x_n(t,e) однородной системы

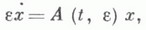
для к-рой справедливо асимптотич. разложение при

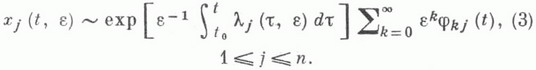
Это разложение равномерно по и его можно дифференцировать по tи по е любое число раз. Если матрица Ане зависит от е, т. е. А=А(t), то

где - левые и правые собственные векторы матрицы A(t), нормированные условием

Решения, имеющие асимптотику вида (3), наз. также ВКБ-решениями (см. ВКБ-метод). Качественная структура этих решений такова. Если

то x_j есть вектор-функция типа пограничного слоя при t₀=0 (t₀=Т), т. е. заметно отлична от нуля только в е-окрестности точки t=0 (t= Т). Если же то решение x_j сильно осциллирует при и имеет порядок O(1) на всем отрезке I.

Если матрица-функция A(t, e) голоморфна при 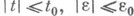и условие 1) выполнено, то формула (3) справедлива при где t₁>0 достаточно мало. Трудной проблемой является построение асимптотики ф. с. р. при наличии на Iточек поворота, т. е. точек, в к-рых матрица A(t,0) имеет кратное собственное значение. Эта проблема полностью решена только для отдельных типов точек поворота (см. [1]). В окрестности точки поворота имеется переходная область, в к-рой решение устроено довольно сложно и в простейшем случае выражается через Эйри функции.

Аналогичные результаты (см. [1]) справедливы для скалярных уравнений вида

где а _j - комплекснозначные функции; роль функций играют корни характерйстич. уравнения

ВКБ-решения возникают также и в нелинейных системах вида

ВКБ-асимптотика (3), в условиях теоремы Биркгофа, справедлива на бесконечном интервале (т. е. разложение (3) - асимптотическое и при и при ), если матрица A(t, е) достаточно правильно ведет себя при 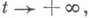напр. быстро стремится к постоянной матрице с различными собственными значениями (см. [2]). К сингулярным задачам с малым параметром приводят многие вопросы спектрального анализа (см. [3]) и математич. физики. 3. Особый интерес представляет исследование нелинейных систем вида

где e>0 - малый параметр. Первое уравнение описывает быстрые движения, второе - медленные движения. Напр., Ван дер Поля уравнение с помощью замены

приводится при больших значениях параметра l, к системе

имеющей вид (4).

При e=0 уравнение быстрых движений вырождается в уравнение f(x, у)=0. Пусть это уравнение имеет в нек-рой ограниченной замкнутой области Dизменения уизолированный устойчивый непрерывный корень x=j(y) (т. е. действительные части всех собственных значений матрицы Якоби отрицательны при x=j(y), ); пусть решения задачи (4) и вырожденной задачи

существуют и единственны при причем получающаяся при решении задачи (5) функция при Если точка ( х ₀, у ₀).принадлежит области влияния корня x=j(y), то

при где - решение вырожденной задачи (теорема Тихонова). Вблизи точки t=0 предельный переход 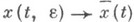является неравномерным - возникает пограничный слой. Для задачи (4) построена асимптотика решения:

а асимптотика для y(t,e) имеет аналогичный вид. В (6) первая сумма - регулярная часть асимптотики, вторая - пограничный слой. Регулярная часть асимптотики вычисляется стандартным способом: ряды вида (2) подставляются в систему (4), правые части разлагаются в ряды по степеням е и затем приравниваются коэффициенты при одинаковых степенях е. Для вычисления погранслойной части асимптотики в окрестности точки t=0 вводится новая переменная t=t/e, (быстрое время) и применяется описанная выше процедура. Возникает нек-рый интервал на оси t, на к-ром пригодно и регулярное (или внешнее) разложение, и погранслойное (или внутреннее) разложение. Функции х _k, П _k определяются из условия совпадения этих разложений (т. н. метод сращивания, см. [4], [5]).

Аналогичные результаты справедливы в случае, когда правые части системы (4) явно зависят от t, для скалярных уравнений вида

и для краевых задач для таких систем и уравнений (см. Дифференциальные уравнения с малым параметром при производных,[6], [7]).

При приближении решения задачи (4) к т о ч к е срыва, где теряется устойчивость (напр., где одно из собственных значений матрицы df/дх при х=j(у).обращается в нуль), ряды вида (5) теряют асимптотич. характер. В окрестности точки срыва асимптотика имеет совершенно иной характер (см. [8]). Исследование окрестностей точки срыва особенно существенно для построения асимптотич. теории релаксационных колебаний.

4. Задачи небесной механики и теории нелинейных колебаний приводят, в частности, к необходимости исследовать поведение решения задачи (1) не на конечном интервале, а на большом, порядка e^-1 или более высокого, интервале по t. Для исследования этих задач широко применяется метод усреднения (см. Крылова - Боголюбова метод усреднения, Малые знаменатели,[9] - [11]).

5. Асимптотика решений уравнений вида (7) исследуется, в частности, с помощью т. <н. метода="" многих="" масштабов="" (см.="" [4],="" [5]);="" этот="" метод="" является="" обобщением="" вкб-метода.="" рассмотрим="" этот="" метод="" на="" примере="" скалярного="" уравнения="">

к-рое имеет периодич. решения (см. [12]). Решение ищется в виде

(функции Т, t наз. масштабами). Если уравнение (8) - линейное, то и (9) есть ВКБ-решение. В нелинейном случае уравнения первых двух приближений имеют вид

причем первое уравнение содержит две неизвестные функции Sи j₀. Пусть это уравнение имеет периодическое по tрешение j₀=j₀(t, Т). Тогда недостающее уравнение, из к-рого определяется S, находится из условия периодичности по tрешения j₁ и имеет вид

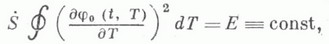
где интеграл берется по периоду решения j.

Лит.:[1] В а з о в В., Асимптотические разложения решений обыкновенных дифференциальных уравнений, пер. с англ., М., 1968; [2] Ф е д о р ю к М. В., "Матем. сб.", 1969, т. 79, № 4, с. 477-516; [3] Н а й м а р к М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [4] К о у л Д.-Д., Методы возмущений в прикладной математике, пер. с англ., М., 1972; [5] Найфэ А. X., Методы возмущений, пер. с англ., М., 1976; [6] Васильева А. Б., Бутузов В. Ф., Асимптотические разложения решений сингулярно возмущенных уравнений, М., 1973; [7] их же, Сингулярно возмущенные уравнения в критических случаях, М., 1978; [8] Мищенко Е. Ф., Р о з о в Н. X., Дифференциальные уравнения с малым параметром и релаксационные колебания, М., 1975; [9] Боголюбов Н. Н., Митропольский Ю. А., Асимптотические методы в теории нелинейных колебаний, 4 изд., М., 1974; [10] В о л о с о в В. М., Моргунов Б. И., Метод осреднения в теории нелинейных колебательных систем, М., 1971; [11] Арнольд В. И., "Успехи матем. наук", 1963, т. 18, в. 6, с. 91 - 192; [12] К у з м а к Г. Е., "Прикл. матем. и мех.", 1959, т. 23, № 3, с. 515 - 26; [13] Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, 2 изд., М., 1959; [14] Д ж а к а л ь я Г. Е., Методы теории возмущений для нелинейных систем, пер. с англ., М., 1979; [15] М о и с е е в Н. Н., Асимптотические методы нелинейной механики, М., 1969; [16] Бутузов В. Ф., Васильева А. Б., Ф е д о р ю к М. В., в кн.: Итоги науки. Математический анализ. 1967, М., 1969, с. 5-73. Н. X. Розов, М. В. Федорюк.

2) М. п. м. для дифференциальных уравнений с частными производными. Как и для обыкновенных дифференциальных уравнений, решения дифференциальных уравнений с частными производными могут зависеть от малого параметра е (предполагается, что e>0) регулярно или сингулярно. Грубо говоря, регулярная зависимость наблюдается тогда, когда старшие члены дифференциального оператора не зависят от e, а младшие члены - гладкие функции e при малых e. Тогда и решение является гладкой функцией e. Если же при обращается в нуль какой-либо из старших членов в уравнении с частными производными, то решение, как правило, зависит от e сингулярно. В этом случае часто говорят об уравнении с частными производными "с малым параметром при старших производных". Подобная классификация несколько условна, т. к. само выделение старших членов не всегда очевидно; к тому же параметр может входить и в граничные условия. Кроме того, сингулярность может возникнуть в случае неограниченной области, даже если малый параметр стоит при младших производных (на бесконечности они играют в определенном смысле такую же или даже более главную роль, чем старшие).

Пусть, напр., имеется эллиптич. уравнение с частными производными 2-го порядка в ограниченной области Решение задачи

есть гладкая функция e при малых e, если граница гладкая, a_j, b, f, j - гладкие функции от x и e и предельная краевая задача

однозначно разрешима для любых гладких функций f(x,0), j( х,0). Решение разлагается в асимптотич. ряд по степеням e:

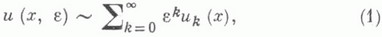
коэффициенты к-рого и _k (х) - решения однотипных краевых задач и легко вычисляются в возмущений теории.

Совсем иная ситуация имеет место, напр., для краевой задачи

т. <к. при="" e="0" порядок="" уравнения="" понижается.="" предельная="" задача="" имеет="" вид="">

и, вообще говоря, неразрешима. Пусть n=2, характеристики предельного уравнения имеют вид, указанный на рис., и их ориентация индуцирована векторным