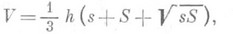-
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.пирамида
пирами́да, -ы -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
ПИРАМИДА - монументальное сооружение, имеющее геометрическую форму пирамиды (иногда также ступенчатую или башнеобразную). Пирамидами называют гигантские гробницы древнеегипетских фараонов 3-2-го тыс. до н. э. (высота пирамиды Хеопса в Гизе 146,6 м), а также древнеамериканские постаменты храмов (в Мексике, Гватемале, Гондурасе, Перу), связанные с космологическими культами. -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.пирамида
-ы, ж.1. мат.Многогранник, основание которого представляет собой многоугольник или треугольник, а боковые грани — треугольники, имеющие общую вершину.Пятигранная пирамида.2.То, что имеет форму такого многогранника.Каждый почти занят был рассматриванием великолепной крепости из сладкого теста с вензелями А и Б, воздвигнутой посредине стола, между бисквитных и сахарных пирамид. Григорович, Проселочные дороги.На север поднялась дикая каменная пирамида горы Развалки. Шулейкин, Дни прожитые.3.Огромное каменное сооружение с четырехугольным основанием и сходящимися к вершине боковыми гранями, служившее гробницей фараона в древнем Египте.На стене, в желтой ясеневой раме, висел чертеж египетской пир…
Далее -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
I ж.1.Монументальное каменное сооружение с четырехугольным основанием и треугольными боковыми поверхностями, образующими на вершине постройки острый угол, служившее гробницей фараонов в древнем Египте.отт. Памятник такой формы, воздвигнутый в память о ком-либо, чем-либо, в честь кого-либо, чего-либо.2.Многогранник, основание которого представляет многоугольник, а боковые грани - треугольники, имеющие общую вершину (в математике).отт. Предмет такой формы.отт. Группа предметов, сложенных в виде такой фигуры.3.Гимнастическая или акробатическая фигура, суживающаяся кверху, составленная из группы людей, становящихся друг другу на плечи.4.Приспособление для установки и хранения винтовок и ружей.II …
Далее -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
пирамиды, ж. (греч. pyramis). 1. Многогранник, основание к-рого представляет многоугольник, а остальные грани - треугольники, имеющие общую вершину (мат.). Пятигранная, семигранная пирамида. 2. Колоссальное каменное четырехгранное сооружение подобной формы, служившее гробницей фараонов в древнем Египте (истор.). В окрестностях Каира до нашего времени сохранилось около 80 пирамид. Я памятник себе воздвиг чудесный, вечный, металлов тверже он и выше пирамид. Державин. 3. перен. Кучка составленных, сложенных вместе предметов, имеющая широкое основание и суживающаяся кверху. Пирамида сухарей (напр. в витрине булочной). 4. Суживающаяся кверху акробатическая фигура из людей, становящихся друг на др …
Далее -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.ПИРАМИДА
ПИРАМИ́ДА, -ы, жен.1. Многогранник, основание к-рого представляет собой многоугольник, а остальные грани треугольники с общей вершиной.2. Предмет такой формы.3. Большое каменное сооружение такой формы гробница фараона 1. Египетские пирамиды.4. Группа предметов, сложенных в виде сужающегося кверху многогранника или конусообразно. Ружья в пирамиде (составленные друг с другом наклонно штыками вверх).5. Гимнастическая или акробатическая фигура несколько акробатов, гимнастов, стоящих друг на друге.6. Станок для хранения винтовок (спец.).| уменьш. пирамидка, -и, жен. (ко 2 и 4 знач.). Детская п. (разборная игрушка).| прил. пирамидный, -ая, -ое. -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.ПИРАМИДА
жен., греч. остряк, островерхое тело на широкой подошве, с откосыми боками; как бы граненная сахарная голова. В геометрии тело, ограниченное равными треугольниками, составленными вершинами в одну точку и образующими основаньями своими угольник. Египетские пирамиды четыреугольные. Пирамидный вход, у египтян, вел к могиле или ко гробу. Пирамидальный памятник. Пирамидальный тополь, южный, крымский, украинский, итальянский или раина. Пирамидальное пирожное. -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
пирами́да народн. перемида, при Петре I (по аналогии образований с приставкой пере-), русск.-цслав. пирамида πυραμίς (Григ. Наз., ХI в.). Из греч. πυραμίς, вин. -ίδα; см. Фасмер, ИОРЯС 12, 2, 265; Гр.-сл. эт. 150. Совр. русск. слово, вероятно, заимств. из зап.-европ. языков – скорее через нем. Pyramide (часто в XVII в.; см. Шульц–Баслер 2, 744 и и сл.), чем из франц. руrаmidе. -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
Заимствовано из старославянского, которым в свою очередь было заимствовано из греческого pyramida (pyramis). -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
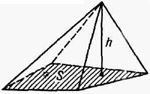
(от греч. pyramis, род. midos), многогранник, основание к-рого многоугольник, а остальные грани - треугольники, имеющие общую вершину (рис.). По числу углов основания различают П. треугольные, четырёхугольные и т. д. Объём пирамиды V=1/3*Sh.
-
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
- многогранник, одной из граней к-рого служит многоугольник (основание П.), а остальные грани (боковые) суть треугольники с общей вершиной (вершина П.) (см. рис. 1, 2). В зависимости от числа боковых граней П. делятся на треугольные, четырехугольные и т. д.
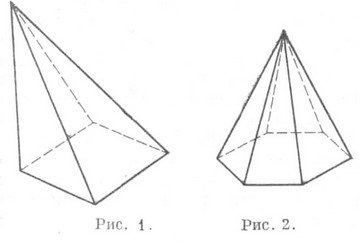
Отрезок перпендикуляра, опущенного из вершины П. на плоскость ее основания (а также его длина), наз. высотой П. Объем П. вычисляется по формуле
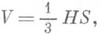
где H - высота, S - площадь основания, П. наз. правильной (см. рис. 2), если в основании ее лежит правильный многоугольник и высота П. проходит через центр основания. Боковые грани правильной П. суть равные между собой равнобедренные треугольники; высота каждого из этих треугольников на
…
Далее -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
[от греч. pyramis (pyramidos)] - многогранник, основание к-рого - многоугольник, а остальные грани - треугольники, имеющие общую вершину (рис. 1). По числу углов основания различают П. треугольные, четырёхугольные и т. д. Объём пирамиды V = 1/2Sh. Если пересечь П. плоскостью, параллельной основанию, то получится усечённая пирамида (рис. 2), объём к-рой V = 1/3h (S1 + корень из (S1S2)+ S,).
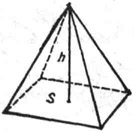
<рис. 1="" к="" ст.="">
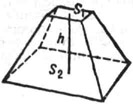
<рис. 2="" к="" ст.="">
-
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Пирамида
- способ незаконного обогащения, используемый финансовыми компаниями. Поступления денежных средств от продажи компанией ценних бумаг лицам, образующим нижние слои П., частично - передаются в виде дивидендов лицам, которые ранее приобрели ценные бумаги и образуют верхушку П., частично идут на широкую рекламу и в доход финансовой компании. П. раньше или позже обречена на разрушение. Участники нижних слоев теряют свои вложения, а компания либо терпит крах, либо приступает к созданию новой П. Законодательством такие финансовые операции обычно запрещены.